Математика тиражных решений — советы в блоге
26 июля 2021
Автор: Потапов Валентин

Мы в whatAsoft очень любим математику и различные задачи. Особенно если они имеют какой-то практический смысл. Как вы знаете, мы выпустили большое обновление нашего интернет-магазина и написали несколько статей о том, что мы добавили (тут, тут, тут и тут). Одной из добавленных фич стала возможность переставлять блоки на главной странице. Интересно, сколько появилось вариантов оформления главной страницы у администратора интернет-магазина после выхода обновления? Для ответа на этот вопрос мы можем использовать такой раздел математики, как комбинаторика.
Комбинаторика — это раздел математики, изучающий дискретные объекты, множества и отношения на них. Комбинаторика используется во многих разделах математики. Например, теории графов, теории вероятностей, алгебры и так далее.
Рис. 1 — Комбинаторика
Итак, исходные данные: 7 блоков, которые можно отключать и менять местами. У нас может меняться не только позиция блока, но также блок может вовсе отсутствовать в итоговом варианте оформления главной станицы.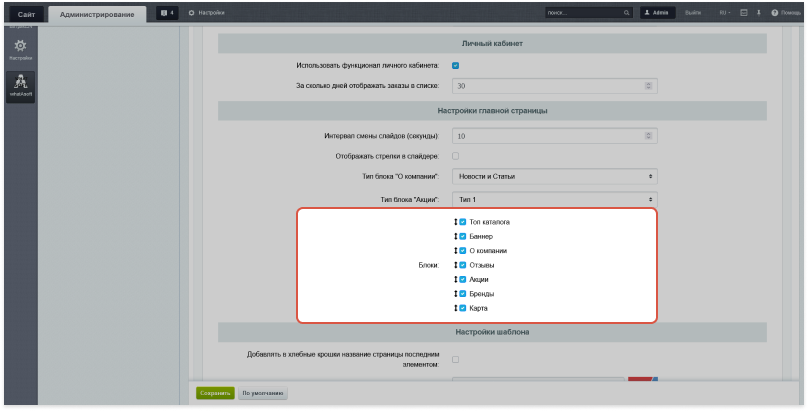
Рис. 2 — Настройка расположения блоков на главной странице
Давайте формализуем задачу. Как известно, в комбинаторике часто оперируют двумя формулами: числа сочетаний и размещений. Да, есть еще и перестановки, но это частный случай размещения m элементов из m-элементного множества.
Звучит, возможно, не просто, но выводы весьма интересны!
Вспомним, что сочетания от размещений отличаются тем, что в размещениях важен порядок, а в сочетаниях нет. Другими словами, сочетания {1,2,3,4} и {1,4,2,3} – это одно и то же, в то время как размещения {1,2,3,4} и {1,4,2,3} будут различными. Значит, в нашем случае, речь пойдет о размещениях, потому как главная страница, в которой сперва идет блок «О компании», а затем блок «Акции» и страница с блоками «Акции», а затем «О компании» – это разные главные страницы. Визуально это хорошо видно.

Рис. 3 — Различие в главных страницах с разным порядком следования блоков
Далее, в комбинаторике принято различать размещения (и сочетания) с повторениями и без повторений. Разница заключается в том, что в случае, когда мы имеем место с размещениями с повторениями, в итоговой выборке нам могут встречаться одни и те же объекты исходного множества (например: {1,1,2,3}). Если речь идет о размещении без повторений, то в любом из размещений могут встречаться лишь уникальные объекты. В нашем случае имеем дело с размещением без повторений. Также вспомним, что число размещений обозначают буквой А, ну а сочетания буквой С. Если нужно указать, что сочетания или размещения будут с повторениями, то над символом А или С ставится черта.
Что является объектами в нашем случае? Очевидно, что блоки, которые мы размещаем на те или иные позиции.
Таким образом, общее число вариантов оформления главной страницы будет равно:
K = A70 + A71 + A72 + A73 + A74 + A75 + A76 + A77
То есть мы можем разместить 0 объектов из 7, либо 1 объект из 7, либо 2 объекта из 7 без повторений и так далее… Раз речь идет о том, что мы размещаем либо один вариант, либо какой-то другой, то мы пользуемся правилом сложения.Осталось вспомнить, как выглядит формула размещений без повторений из n по k (Ank). Либо получить эту формулу, используя правило умножения. А именно, руководствуясь тем соображением, что на каждую следующую позицию мы можем выбрать из множества на 1 элемент меньшего, чем мы выбирали на прошлом шаге, мы получим формулу:
Ank = n*(n-1) *(n-2)*…*(n-k+1), что можно переписать как n!/(n-k)!
Собираем все в одно выражение:
K = 7!/7! + 7!/6! + 7!/5! + 7!/4! + 7!/3! + 7!/2! + 7!/1! + 7!/0!
Берем в руки калькулятор и вычисляем, не забывая, что 0! по соглашению равен 1.
K = 1 + 7 + 42 + 210 + 840 + 2520 + 5040 + 5040 = 13 700
То есть существует 13 700 различных вариантов главной страницы, которые могут быть получены администратором сайта, если он воспользуется механизмом выбора блоков на главной. Довольно большое количество вариантов.Если добавить к этому возможность выбора одного из шести вариантов оформления главного меню, то получится уже 6 * 13 700 = 82 200 вариантов главной страницы.
Давайте оценим это число: предположим, вы собираетесь выбрать один из вариантов. На просмотр каждого вы тратите 23 секунды (кровь совершает полный оборот в организме за 23 секунды, значит мы будем смотреть каждый способ в одинаковых условиях).
Вы потратите примерно 22 дня!
Ну а если распечатаете (по три странички на вариант, на офисной 80-граммовой бумаге) вам понадобиться всего 1230 килограмм бумаги (и много картриджей).
Как видите, несмотря на то что многие относятся к тиражным решениям, как к шаблонам, противопоставляя этому разработку уникальных сайтов, при правильном подходе вы можете настроить сайт таким образом, что найти идентичный сайт, который запущен на таком же решении, будет сложно. Вот такая занимательная математика и удивительные выводы!
А еще сайт становится уникальным в первую очередь благодаря оригинальному контенту, а не индивидуальному дизайну.
Статья полезна для



